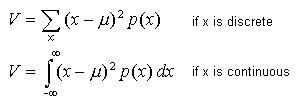
Standard Deviation

The variance of a variable X with probability distribution p(x) is given by:

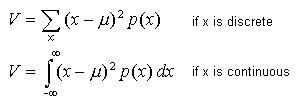
where m is the mean value.  The variance of a probability distribution isn’t exactly the same as “sample variance”, which is the variance of a set of measurements.

The standard deviation is the square root of the variance.  Its units are the same as those of X, and it is a measure of how “spread out” or “imprecise” the distribution is.

For any distribution, the mean (i.e., the expected value) and the median can never differ from each other by more than one standard deviation.

For a normal distribution, 31.8% of the probability is outside of 1 standard deviation from the mean, 4.6% is outside of 2 standard deviations, and 0.26% is outside of 3 standard deviations. For any distribution, less than 1/(k^2) of the probability is outside of k standard deviations (Chebyshev’s theorem).