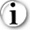
Pareto Distribution |
(continuous probab dist for equations) |
Usage: |
ParetoDist (x, a, b) |
Definition: |
(a/b) (b/x) ^ (a + 1) |
Parameters: |
a is shape b is location |
Required: |
a > 0 b > 0 |
Support: |
x ⋝ b |
Moments: |
μ = a b / (a-1) for a > 1 (∞ for a ⋜ 1) σ^2 = a b^2 / [(a - 1)^2 (a - 2)] for a > 2 (∞ if 1 <a ⋜ 2, non-existent if a ⋜ 1) γ1 = [2(1 + a)/(a - 3)] sqrt ((a - 2)/a) for a > 3 β2 = 6(a^3 + a^2 – 6a - 2) / [a (a - 3) (k - 4)] for a > 4 |
The Pareto distribution is a power law probability distribution found in a large number of real-world situations, such as the distribution of wealth among individuals, frequencies of words, size of particles, size of towns/cities, areas burnt in forest fires, size of some fractal features etc. These are situations where there are many that are small and a few that are large (like the "Pareto principle", in which 20% of the population owns 80% of the wealth).
For any value of a, the distribution is "scale-free", which means that no matter what range of x one looks at, the proportion of small to large events is the same (i.e., the slope of the curve on any section of the log-log plot is the same).
Also known as the Bradford distribution.