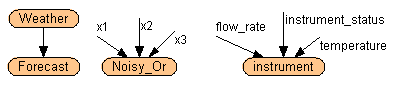
Often the probabilistic relation between a node and its parents represents a small piece of local knowledge which may be applicable in a number of different nets to be used in different situations. That relation may have been learned from data, or entered by an expert. Each new net that it is placed in captures the global relations between such local pieces of knowledge, and belief updating combines the local and global knowledge with the details of some particular case.
You can keep pieces of local knowledge as net fragments in a net library, and later paste them into nets you design to solve a particular problem. Here is an example of a few net fragments in a library:
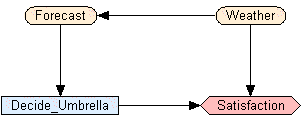
Example: For example, suppose that you made a simple net consisting of a node called Forecast connected to a node called Weather (what the weather turned out to be after the forecast). You could put the link between them either way, since in this situation you can’t really capture causation (they are both caused by other variables, such as the weather at earlier times), but say you put the link from Weather to Forecast because often its better to put links from more immutable to less immutable variables. You could learn its probabilities from a set of cases consisting of the forecast and what the weather turned out to be. Then you could put it in a library where it might look like the leftmost fragment in the diagram above. Later, you graft it into nets for inference involving the weather and its forecast, such as the decision problem example:
Example: As another example, suppose you have a device for measuring the flow rate in a pipe. It produces biased readings depending on the ambient temperature, and it can malfunction in a few different ways, each of them producing wrong or inaccurate readings. You can model the device with a 4 node net, consisting of one node for the reading on the device, and 3 parent nodes corresponding to: actual flow rate, ambient temperature, and device status (okay, broken 1, broken 2, etc.). You enter the probability table, and then you disconnect the node from its parents and place it in a library. The rightmost node in the first diagram on this page shows how it will appear.
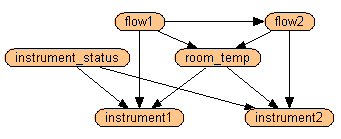
Later, if you have a net to model a situation in which you use the instrument to make two measurements of the flows in two connected pipes located in the same room, you just duplicate the device characteristics node from the library twice into the new net, and graft it to the appropriate nodes in that net, as shown in the diagram below. Note that if the ambient temperature could be different between the two measurements, then the room_temp node would appear as two connected nodes, similar to the flow nodes, and the same goes for the instrument_status node if the device may have broken between measurements.